I want to bring together a number of thoughts in this blog, most importantly the idea that as the practice of supply chain management has aged, there is a more rounded approach to the education and training of people entering the practice. Lora Cecere’s view is that we are entering the 3rd generation. I hope so because, by Lora’s definition, I am 2nd generation and I had a far too narrow education. Perhaps this was more a reflection of my choices than what was available, but I did take English, History of Art, German, and Philosophy as electives during undergrad and grad school. But I never took Finance or Accounting. I could have taken some Biz Studies courses, but I thought these were way too applied. I wanted ‘hard science’; things with differential equations and mathematical optimization. There was a Finance in Engineering course that was considered an easy option, but there were very few girls who took the course. Oh well, that wasn’t the only mistake I made in the past that was based more on testosterone than an understanding of skills or knowledge I needed to acquire.
Over the years, I have come to understand and appreciate the importance of financial outcomes, but I was well into my 30’s before I could read a financial statement. In truth, it was probably a few years after that before I understood what lay behind a financial statement. And being self-taught, I have no doubt that there is much I still do not understand. But I would still rate my knowledge to be well above average amongst the self-taught supply chain community that studied one form or another of engineering or computer science. And that is a pity. But this blog isn’t about education for supply chain or finance for engineers. It is about how one narrow aspect of financial analysis taught me to view supply chain decisions differently, Real Options Analysis. As I have commented in the past (I am adamant that an accurate forecast does not reduce demand volatility), a tipping point in my life was when I understood the effect uncertainty or randomness has on our ability to analyze a situation with any degree of precision. I have come to the conclusion that other than for high-level network design or very detailed production planning/sequencing, optimization techniques have a limited application in supply chain management. I had got to this point because:
- There is very limited capability to represent uncertainty in linear programming (LP, IP, or MILP), or there was in the early 1980’s when I was studying this stuff
- Nearly all variables, such as lead time, throughput, and demand have some level of uncertainty to them, often quite a lot
- I had come to realize that these techniques force you to linearize highly non-linear systems, such as manufacturing or supply chains
- Which is adding approximation to uncertainty
- All optimization techniques force you to select some common unit-of-measure, usually money, for the objective function
- This necessitates the development of 'factors' to convert operational measures, such as customer service, into a currency, when this relationship is not proven, known, linear, or static
As part of my graduate research I had come to the conclusion that I had to use some modeling tool that allowed me to incorporate uncertainty and that also did not force me to linearize the system I was modeling, which made me investigate discrete-event simulation tools. From an optimization perspective I had to adopt pattern search techniques, such as Hooke-Jeeves. I was familiar with both non-linear systems and search techniques from my Chem Eng background but this was a whole new world for the Industrial Engineering department, while the IE department knew a lot more about uncertainty than I did as a Chem Eng. There was some vigorous discussion with my committee and advisor because the purists did not see search techniques as real optimization. The pivotal point was when I convinced them that if the model is not sufficiently accurate you can't prove that you have found the optimum - max or min - anyway. They reluctantly allowed me to continue with my 'practical' research as opposed to a more theoretical approach, because at the heart of my research was the understanding of risk, which I thought was a novel approach at the time. Once I managed to hook up the discrete-event model with the optimization technique it was taking over 40 hours to run an optimization of a fairly simple manufacturing cell with 5 machines, 3 operators, and 50 SKUs. Obviously this was way too long for practical use. That didn't matter in academia, but it did matter to me, and it did matter to the manufacturing company with whom I was working. From an academic perspective, the interesting outcome was that the shape of the result was like a bath tub. In other words, there was a huge area where you couldn't tell with 80% confidence where the true optimum lay, which meant you could select a wide range of values for the input variables without having a measurable effect on the result. Using a 95% confidence level only makes the bottom of the bath tub even wider. I then investigated the effect the degree of uncertainty/randomness of the input variables had on the shape of the objective function. Unfortunately it was more than 1:1 and it was not linear. Even if I made all but one input variable fixed - I chose to keep production rate variable - the degree of uncertainty in the objective function was greater than the degree of variability of the input variable, and as the variability increased the degree of uncertainty went up faster. Using the analogy of a bath tub implies that there are only 2 input variables when in fact there are many. In a multi-tier supply chains there are thousands. As an example of real-world variability, at a recent supply chain conference someone from one of the leading CPG companies said that their monthly demand Coefficient-of-Variation (CoV = std. dev./mean) for many of their high revenue items is over 1.5, largely because of the effects of seasonality coupled with promotions. He said if anyone in Operations thinks that either seasonality or promotion planning is going to decrease they are delusional. CoV should not be confused with forecast accuracy, but higher CoV usually results in lower forecast accuracy. And a CoV of 1.5 is very high. But a CoV of 3 is not unusual for NPI. So even if we have a perfectly accurate model of our supply chain, how optimal will be the supply plan? This was the problem I was trying to address in my research.
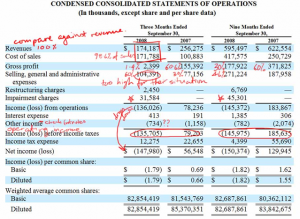
I was still forced to use an objective function, despite all the drawbacks this implies. I wish I had known then what I know now about accounting because I would have tried to use something like Return-on-Assets (ROA) as the objective function. But the issue with something like ROA is that it is affected by the cost accounting method used. (By the way, I am certain that there is at least one Finance or Accounting person out there whose toes are curling while reading my simplistic explanation.) The objective function for a fixed cost allocation method will give very different results from a variable cost method. But at least it would be consistent with the company's financial accounting methods, and understood by Finance. Instead, most objective functions are only understandable by the team that wrote the original optimization and therefore is not changed - because it takes too long to change - as market conditions and/or company objectives changes. Actually, I question whether the objective functions developed by Operations people ever matched the company's financial objectives. I have come to adopt Warren Buffet’s (amongst others) mantra, namely that it is better to be approximately right than precisely wrong. I believe much more in being directionally correct. So how can we use this to make everyday decision in the supply chain? One of the most common forms of analyzing the future value of an investment is Discounted Cash Flow (DCF). Of course any decision we make in supply chain planning is an investment decision, even though our decisions are not usually viewed from this perspective. The reality is that in planning we are choosing to invest
- cash in materials we buy,
- productive capacity in the converting the materials we buy into items we sell,
- people in managing the supply chain, and
- sales and promotion funds in getting the product into customers hands.
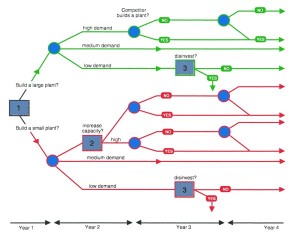
DCF is usually used to analyze capital investments, not operational investments. All our decisions should be evaluated using DCF. But DCF has a fundamental flaw, namely that it is the analysis of the most probable outcome, and I have just spent a page explaining that the market is highly variable and uncertain. So how do we understand the most probable outcome? I have come to see Real Options Analysis as a better form of analysis than optimization, because it incorporate the concepts of uncertainty and likelihood. Here are some links to videos on YouTube: Link 1, Link 2. But a fundamental flaw in Real Options Analysis is that it assumes that you know the probability of an outcome before the fact, for example how well a product will be adopted in the market. If we did know outcomes before the fact we would all be rich. More importantly, the first video outlines the need for continuous adjustment of a plan - whether long term, medium term, or short term – as we gain more information. In the first video, the speaker refers to this as Monte Carlo simulation, which is really just a way of automating what-if analysis. In fact, the third video points to a decision tree, which is essentially a what-if analysis of scenarios and outcomes. This is where human judgment or experience comes in. There is still – more correctly there should still be - a place for human judgment in our decision making processes precisely because of the uncertainty. Scenario analysis, or what-if analysis, is a key capability in which people can perform an analysis of the likely outcome of a set of choices or decisions. Human judgment can be applied to evaluating the likelihood of achieving the outcome, in other words the risks associated with an outcome. But without the ability to evaluate different options quickly across multiple metrics – both financial and operational – it is difficult for a team to arrive at a conclusion of the best way forward that balances opportunity with risk. Lastly, I just want to go back to a key point about Real Options Analysis, namely the continual reevaluation of the options as more market information is received. If we bring the concepts together they add up to Know Sooner; Act Faster.




Leave a Reply