A few weeks ago, Trevor Miles wrote a blog series entitled, “Truth, Lies, and Statistical Modeling in Supply Chain: Part 1, Part 2 and Part 3.
In it, he discusses how companies often model manufacturing and supply chain systems using deterministic models, when in fact everything around us is stochastic. I thought it’d be important to mention that we also model project management using deterministic models, such as the Critical Path Method (CPM). Yet, we are living in a world where projects and tasks might actually follow a stochastic trend. An alternative to CPM is Program Evaluation and Review Technique (PERT), which is an effective method and gives you room to include as much variation into your projects as you want. It is used to analyze and evaluate the time needed to complete tasks in a given project, as well as to identify the minimum time needed for the completion of that project. We know that a single task or project can be delayed for many reasons, such as unforeseen events, which force project managers to tie tasks to completely different predecessors or successors. This randomness forms a very important aspect for project management systems. We simply cannot assume any given project will be managed according to the targets set at the beginning of that project. CPM was developed by Du Pont in 1960 and the emphasis was on the trade-off between the cost of the project and its overall completion time (e.g. for certain activities it may be possible to decrease their completion times by spending more money - how does this affect the overall completion time of the project?). CPM is used in production management for jobs that are repetitive in nature where the activity time estimates can be predicted with considerable certainty due to the existence of past experience. When we look at the CPM being commonly used today, we see there’s something missing. This is due to the fact that CPM uses a deterministic model, which only incorporates a fixed time estimate for each activity. Although this is pretty easy to implement, it’s not sufficient for big-scale projects which can get complicated (and more variable) over time. PERT was developed in 1958 by the US Navy for the planning and control of the Polaris missile program. The emphasis for this model was on completing the program in the shortest possible time. In addition, PERT had the ability to cope with uncertain activity completion times (e.g. for a particular activity the most likely completion time is 4 weeks, but it could be anywhere between 3 weeks and 8 weeks). PERT is often used in project management for non-repetitive jobs, for example, research and development work, where the time and cost estimates tends to vary. PERT uses beta probability distribution, which in its essence, models the behavior of random variables and can be implemented by either using the statistical probability theory or discrete-event simulation. The way it is used in project management is through calculating the time allocated (Expected time) for the completion of a given activity. The way PERT deals with variation is its main differentiator. You determine the probability of any given activity to be successfully completed within three time estimates - optimistic (shortest), most likely and pessimistic (longest) times. These estimates (called random variables) represent the reasonable values you can give as the rate at which an activity can be possibly completed. Then, these time estimates are used in a weighted average assuming a beta probability distribution, and this weighted average forms the Expected time for a given task. Here`s how the Expected time is calculated:
Expected time = (Optimistic + 4 x Most likely + Pessimistic) / 6
Let’s dig into some background information now:
Pert Beta Distribution uses three parameters:
a: the optimistic time, which will be required if activity execution goes extremely well
m: the most likely time, which will be required if activity execution is normal
b: the pessimistic time, which will be required if everything goes badly
Depending on the values provided, the Pert Beta distribution can provide a close fit to the Normal or Lognormal distributions and it has:
Mean = (a + 4m + b) / 6
Standard Deviation = (b – a) / 6
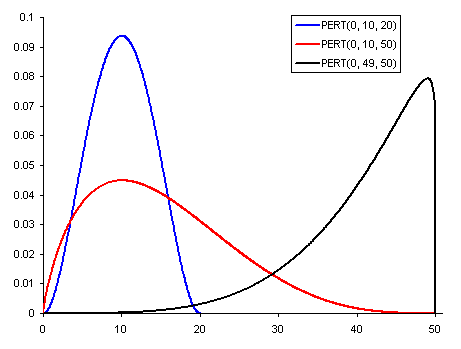
Pert Beta distribution emphasizes the “most likely” value over the minimum and maximum estimates. It constructs a smooth curve which places progressively more emphasis on values around (near) the most likely value, in favor of values around the edges. In practice, this means that we “trust” the estimate for the most likely value, and we believe that even if it is not exactly accurate (as estimates seldom are), we have an expectation that the resulting value will be close to that estimate. Assuming that many real-world phenomena are normally (or log normally) distributed, the appeal of the Pert Beta distribution is that it produces a curve similar to the normal (lognormal) curve in shape, without knowing the precise parameters of the related normal (lognormal) curve. The figure below shows three such distributions.
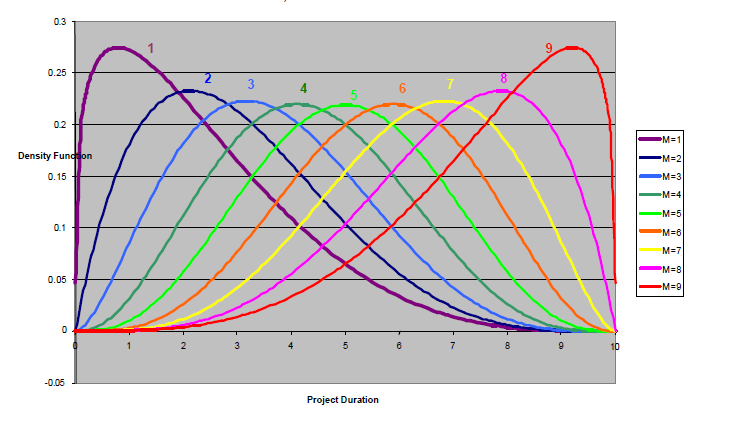
As I said, Pert Beta distribution emphasizes the “most likely” value over the minimum and maximum estimates. The figure below illustrates this effect and shows the various density function shapes that occur as m varies from 1 to 9 when a is 0 and b is 10.
Let's now take a look at some characteristics:| CPM | PERT |
| Deterministic | Probabilistic |
| Estimates are based on historical data | Estimates are uncertain, there`s a probability that an activity will fall into a certain range |
| Concentrates on Time/Cost trade off | More suitable for planning |
| Scalable for smaller projects | Suitable for R&D projects |
| Explicit estimates on time and cost | Includes subjectivity, depends on judgment for optimistic/pessimistic time estimates |
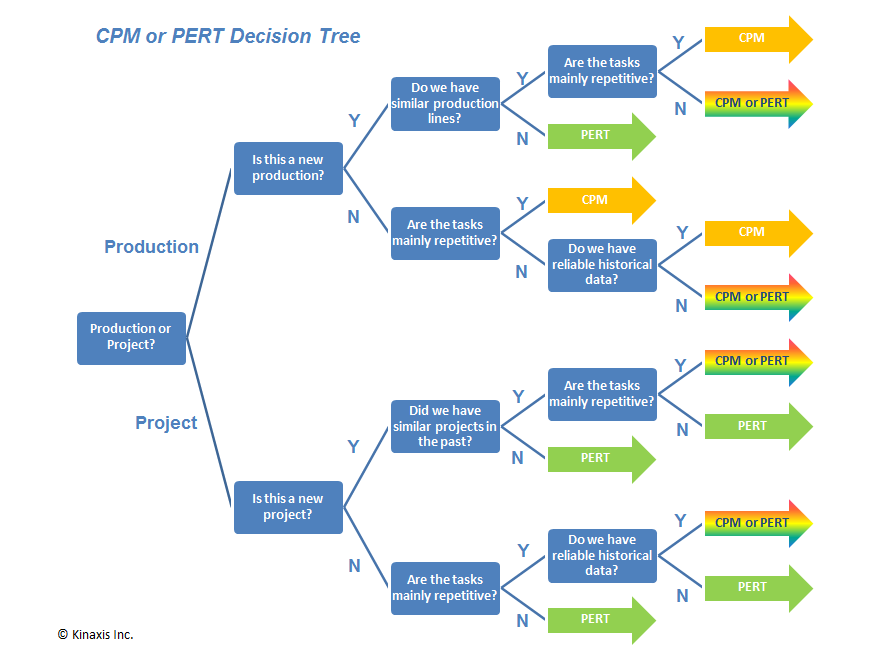
So knowing the characteristics of these two different models, which one do you really need to implement? This totally depends on what type of project you are dealing with. Since PERT concentrates on variation and thus gives you the ability to be more flexible time wise, an R&D project would be a good fit considering the uncertainties a development work could have in the earlier phases of the project. The following decision tree model can help you answer this question.
Still undecided? Well, consider that PERT can answer questions not applicable in CPM such as:- What is the probability that my task will take longer than...?
- What is the probability that my task will be finished by...?
And, PERT can also be used for risk analysis and to identify potential opportunities and difficulties for the activities, as well as for the calculation of the worst case scenario. Imagine a famous band going on a world tour. They are on their way to play another concert that day in a neighboring country, but production trucks cannot cross the border because there is a strike at the border of the country they are currently in. To make it in time to perform, the truck has to cross the border by a certain time. In such a case, it’s out of the organizer’s (or project manager’s) control to project how long it will take until the production truck makes it to the concert area. To avoid such a situation, it’s more realistic to have implemented PERT, allowing some buffers between ongoing tasks, much like transporting rock stars between concert venues. If you are managing a more conventional project with more predictable durations that can be accurately calculated and there’s no need to factor a possibility of changing requirements, then CPM is a good fit. For all other cases (and there would be many!), I recommend going with PERT. After all, like the transportation algorithm is a special case of the regular simplex method, CPM is simply PERT where a = m = b.





Discussions
Thank you very much for sharing this.
Educating our executive managers, the majority of whom have had no formal training in project management techniques, should be our number 1 objective but as with all human endeavours, it's a very problematic path
Dave
Leave a Reply