As discussed in Part 1 and Part 2 of the "Truth, Lies, and Statistical Modeling in Supply Chains series, systems rarely exhibit variability that follows a Normal distribution, even though very often we base our inventory policies on the assumption that both demand and supply lead times follow a Normal distribution.
In this blog, I want to address the issue of the effect variability has on capacity needs. This is where Queuing Theory comes in handy, though let me start by admitting that Queuing Theory can only take us a little way down the road of understanding some fundamental principles and is next to useless to evaluate and manage something as complex as a supply chain. In fact, the mathematics for anything more complex than even a single server and single arrival is daunting, and even then we need to make some pretty radical assumptions. But, nevertheless, there are some really valuable ideas that come out of this analysis. As I mentioned way back when in a blog titled “I am adamant that an accurate forecast does not reduce demand volatility”, my first degree was in Chemical Engineering, a rigorous and very mathematical course that does not admit to any randomness in the chemical processes. As a consequence, when I took a course in graduate school in which the lecturer asked us on the first day how long the queue/line would be if she took about 1 minute to check our IDs and people arrived to the class at approximately 1 person per minute, my immediate reply was that there wouldn’t be a queue because the moment she was finished checking one ID the next person would arrive.
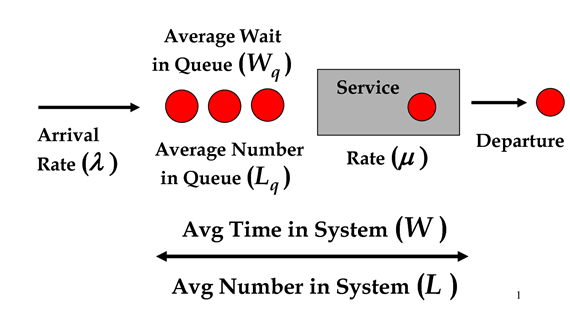
Wrong. Because of those words ‘about’ and ‘approximately’. So let’s dive in and see what this means. To make the mathematics at least workable we need to make 2 major simplifying assumptions, namely that people arrive at class completely randomly – no friends walking to class together – and that it takes next to no time to check most IDs but occasionally it takes a long time to check an ID. In other words, the time it takes to check the IDs follows an Exponential distribution with an average service time of 1 minute. So, an Exponential distribution has a similar shape to a LogNormal distribution with a high Coefficient of Variation (CoV). In fact, the time between people arriving to class will also follow an Exponential distribution. In the diagram we can see all the elements and characteristics of this very simple Queuing System where:
- λ = rate of arrivals, which is 1 per minute in the example above
- µ = service rate, or time to check IDs, which is 1 per minute in the example above
We can then derive equations to calculate all the other resultant characteristics of Wq, Lq, W, and L. This is where assuming an Exponential distribution comes into play because assuming a distribution with a more complicated probability density function makes it really difficult – some would say impossible – to derive the equations for Wq, Lq, W, and L. In the case where both arrivals and service follow Exponential distributions these are:
- L = λ / (µ - λ)
- Lq = λ2 / µ(µ - λ)
- W = 1 / (µ - λ)
- Wq = λ / µ(µ - λ)
In the example above, µ = 1 and λ = 1 therefore (µ - λ) = 0, meaning that all the characteristics above will be infinite. In other words, the queue will grow infinitely, as will the waiting time in the queue. This was pretty counter intuitive to me and it took me a long time, and many hours in the computer lab, to accept that this is correct. Let’s look at the problem from a different perspective. How quickly do we need to be able to check the IDs to ensure that there are no more than 10 people in the queue? Well, we have to formulate the question slightly differently, namely that the probability that there are “k” or more people either in the queue or having their ID checked is:
P(n>k) = (λ / µ)k
So, the probability that there are fewer than “k” people in the queue is:
Pq(n<k) = 1 - (λ / µ)k+1
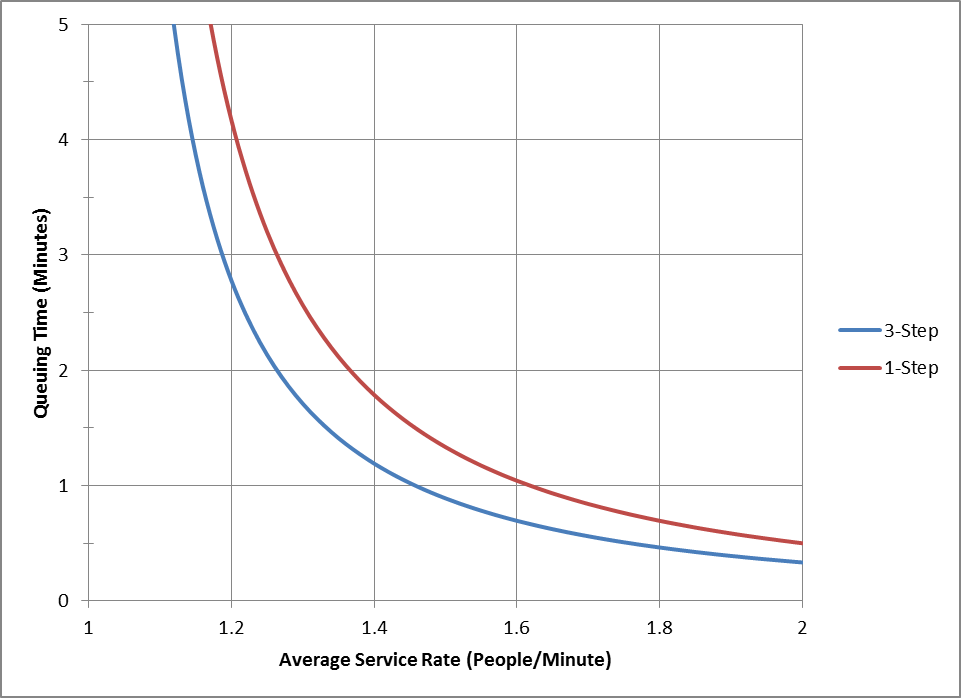
To be 95% sure that there are 10 or fewer people in the queue, we need an average service time of about 45.7 seconds, meaning that close to 25% of our capacity is used to buffer against service variability. The average waiting time in the queue would be about 146 seconds. To be 99% sure that there are 10 or fewer people in the queue, we need a service time of about 40 seconds, meaning close to 33% of our capacity is used as a buffer. The average waiting time in the queue, in this case, would be about 76 seconds. In other words, an enormous amount of extra capacity is required to absorb demand and supply variability while keeping the queue size small and the queuing time low. But this is a very simplistic case with a single queue, a single process, and a single server. Imagine now that checking IDs is a 3 step process carried out by the same person, and each step follows an Exponential distribution. In this case to get an averaging queuing time of 1 minute or less, we need an average service time of about 41 seconds; And to get a queuing time of 30 seconds or less, we need an average service time of about 34 seconds, or very close to 50% capacity utilization. Of course, most of the time our service rates are not as variable as is modeled by an Exponential distribution, but, on the other hand, the structure of a supply chain or manufacturing process is a lot more complex than a single server system with a single queue. And the sources of variability are a lot more varied than can be captured in a single service time because of factors such as change-overs, failures, yield, and learning. It is not difficult to see that variability will reduce the effectiveness of capacity very quickly, especially when companies are pressed to reduce working capital by reducing inventory. This shifts the investment from inventory (OpEx) to capacity (CapEx). The same argument can be made on the demand side where there are so many factors that influence demand, many of which are not considered in a forecast based upon historical shipments. This is why I spent so much time in Part 1 proving that in many, many cases demand and supply quantities and lead times do not follow a Normal distribution. Part of the reason I emphasized the LogNormal distribution in the first blog of this series is that with a high CoV it approximates an Exponential distribution very well. Given the debilitating effect of variability on available capacity, it is very easy to see why, whether based on Queuing Theory or through experience, so much of Lean and Six Sigma is focused on reducing variability. If only it were so easy to predict and eliminate variability. More blogs in this series: Truth, Lies, and Statistical Modeling in Supply Chain – Part 1 Truth, Lies, and Statistical Modeling in Supply Chain – Part 2
Additional Resources
- Inventory optimization frequently asked questions




Discussions
So if it takes you a week to realize in customer facing roles that there is a 'wrench' in production, you will need big buffers. But it only takes a few minutes, you will need smaller buffers.
Regards
Trevor
The answer is to use segmentation analysis to identify the customers or regions that contribute to the long tail. And then use postponement for the 'long tail' to the right of the mean. This may increase delivery lead times or cost fi you use a faster delivery mechanism. You can then remove that demand from the analysis of the inventory needs at a forward location and only focus on the demand around the mode of the LogNormal. This will reduce your inventory tremendously, but increase either your delivery lead time or cost, for some demand.
Regards
Trevor
Leave a Reply