One critical aspect of supply chain planning is the determination of how to allocate limited supply to volatile demand. While the COVID-19 pandemic has certainly highlighted the importance of solving this problem, dealing with shortages is something supply chain planners have always had to deal with for virtually every type of finished good: from toilet paper to gasoline; from life-saving vaccines to graphics cards; and from ice cream to cars.
Of course, if at least some supply is available, it’s likely that not every demand will be completely late or unsatisfied. Put another way, not all demands are equal. For example, a sales order due next week should probably not be sacrificed in favor of a forecast one year from now.
Let’s explore some of the ways that we can algorithmically allocate supply to demand. Consider the following example:
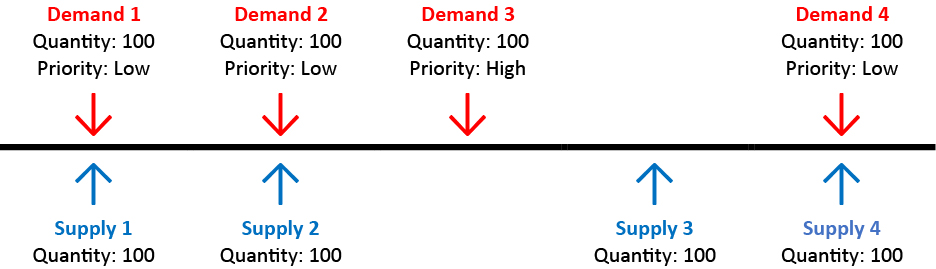
In this diagram, time moves forward along the horizontal axis day by day. The red arrows represent demands throughout the planning horizon, while the blue arrows represent available supplies. Our task is to match supplies to demands.
Method 1: Date sequence
Perhaps the simplest way to solve the problem is to iterate through the demands one-by-one in date sequence and assign them to the next available supply. Doing so here would match Demand 1 with Supply 1, Demand 2 with Supply 2, Demand 3 with Supply 3, and Demand 4 with Supply 4.
Is this a good solution? Let’s first look at the impact on our demands:
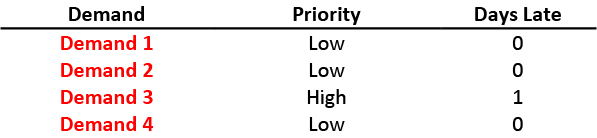
This solution results in only a single day of lateness, but this came at the cost of the highest priority demand in the planning horizon. Perhaps the simplest way was a bit too simple.
Method 2: Priority sequence
If assigning the demands in date sequence resulted in leaving high priority demands unsatisfied, it might seem natural to try assigning in priority sequence instead. In cases where two demands have the same priority, we consider the earlier of the two demands to have higher effective priority to break the tie.
Applying this strategy to our example means that we would first satisfy Demand 3 using Supply 1, the earliest available supply. Similarly, we then match Demand 1 with Supply 2, Demand 2 with Supply 3, and finally Demand 4 with Supply 4, giving the following result:

We achieved our goal of satisfying the high priority demand on time, but it came at the cost of an increased total lateness from one day using Method 1 to three days using Method 2. This is a high cost to pay!
Digging deeper, there is a second undesirable property of this plan. By allocating Supply 1 to Demand 3, we tie up available supply for two days before it is used (or, alternatively, we ship out the supply early and the recipient needs to store it somewhere, which might not always be desirable or even possible).
One possible remedy for the short-term excess issue is to instead allocate the latest available on-time supply instead of the earliest available supply. Unfortunately, this approach runs the risk of not burning off on-hand inventory quickly enough since it naturally avoids earlier supplies. This can result in even more extreme short-term excess in some cases.
Method 3: Hybrid approach
The need for a different approach is clear: the previous two methods either sacrificed high priority demands or too many low priority demands. What have we learned?
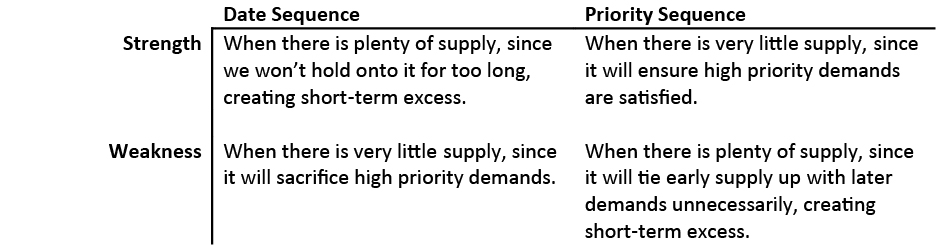
The key is to be able to distinguish between these two cases easily. One way to achieve this is to plan backwards: by working from the latest demand to the earliest demand, we’ll be able to know if we have enough supply at any given time. In cases when we don’t, we can instead use it to satisfy the lowest priority outstanding demand. We will maintain two lists of demands: one sorted by descending due date, and the other sorted by descending priority (again, breaking ties by descending due date). We also maintain a list of supplies sorted in descending order of availability.

Let’s try this approach:
1. Take the next demand from the Demands (Due) list and the Supplies (Available) lists: Demand 4 and Supply 4. Since Supply 4 is not late for Demand 4, we match them.
2. Take the next demand from the Demands (Due) list and the Supplies (Available) lists: Demand 3 and Supply 3. In this case, Supply 3 is late for Demand 3 and so we should try to avoid matching them. Instead, we take the next demand from Demands (Priority) list, which is Demand 2 (since Demand 4 has already been satisfied). We now match Demand 2 and Supply 3. This still introduces lateness, but it is lateness for the lowest priority outstanding demand.
3. Take the next demand from the Demands (Due) list and the Supplies (Available) lists: Demand 3 and Supply 2. Since Supply 2 is not late for Demand 3, we match them.
4. Take the next demand from the Demands (Due) list and the Supplies (Available) lists: Demand 1 (since we have already satisfied Demand 2) and Supply 1. Since Supply 1 is not late for Demand 1, we match them.
The result is:
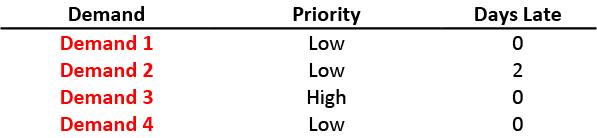
We’ve improved over Method 1 by ensuring the high priority demand is satisfied on time as well as over Method 2 by reducing the total number of days lateness. Furthermore, we never need to hold onto supply longer than one day (the earliest supply is Supply 2, matched to Demand 3).
What has been described here is a basic form of first-come, first-served supply/demand allotment that considers dates and priorities. In realistic supply chains, there are many more wrinkles: fair sharing of lateness, balancing safety stock attainments, and supply expiry, just to name a few.
If you’re interested in helping Kinaxis solve problems like this one, please reach out to us! You can visit our Careers website at https://www.kinaxis.com/en/careers to check out open roles for positions that tackle this and many other problems.


